Правило треугольника: 2academy — LiveJournal

Оригинал взят у palaman в Правило треугольника

Я продолжаю потихоньку развивать тему, которую начал в полушуточном цикле «Математическая конфликтология». Я взял за основу простейшую математическую модель многостороннего конфликта как графа и до сих пор рассматривал лишь случаи простейших конфликтов, которые описываются двудольными графами.

Если говорить попросту, без математического выпендрёжа, речь шла о ситуации, когда участники многостороннего конфликта разделяются на две команды таким образом, что внутри каждой команды конфликты не происходят, гасятся или сводятся к минимуму, так что война происходит по сути между двумя командами.
Такой многосторонний конфликт оказывается в действительности двусторонним

Ясно, что конфликты такого типа являются простейшими случаями с точки зрения конфликтологии. Когда я взялся изучать историю Средневековья, меня очень порадовал тот факт, что в большинстве случаев картина оказывалась именно такой — простейшей (см. например). Это показало мне, что я на верном пути. Когда (в физике) математическая модель выбрана удачно, то в большинстве реальных случаев все сводится к чему-то простейшему.

Но вообще-то основное назначение математики — анализ сложностей через редукцию к простому, так что если направление выбрано верно, то надо потихоньку двигаться дальше, в сторону нарастания сложности модели.

Одно из возможных направлений движения — рассмотреть теперь чуть-чуть более сложные конфликты, несводимые к двусторонним. Рассмотрим для начала конфликты трехсторонние. Речь идет о случае, когда имеется три попарно противостоящих друг другу команды.

В общем случае речь идет о трехцветном графе. Описываемая им политическая ситуация может быть сколько угодно сложной,

но всегда обладает таким свойством, что её участников можно раскрасить в три цвета таким образом, что никакие два участника одного цвета не будут в конфликте между собой. То есть, фактически речь идет о трех попарно враждующих партиях, внутри каждой из которых конфликты отсутствуют или гасятся (элитой данной партии).

Если вдуматься в политический смысл такой ситуации, то придется признать, то разумная тенденция здесь должна быть к замирению.

В самом деле, каждая сторона трехстороннего конфликта заинтересована в том, чтобы обострить взаимный конфликт двух других и занять классическую для политологии позицию «третьего радующегося». Надо даже ожидать, что она будет намеренно разжигать такой конфликт, провоцировать его, чтобы её противники максимально ослабили и истощили друг друга во взаимной вражде.

И значит, каждая сторона (A), в свою очередь, заинтересована и в том, чтобы не поддаваться на провокацию, не позволять другому участнику (B) поссорить его с третьим (C). Потому в подобных случаях можно ожидать возникновения устойчивого равновесия, мира!

Применительно к реальной ситуации в современном мире, можно предположить, что «мир» и «дружба», которые стали причиной столь скоропостижного конца Советского периода истории России, в действительности объясняются тем, что политическая ситуация в мире структурно изменилась. Глобальный мировой конфликт стал из двустороннего трехсторонним.
Я говорю, конечно, о появлении Евросоюза. Кто бы, какой бы противник Штатов ни стоял за спиной СССР, в ситуации появления и резкого усиления третьей силы этот кто-то (а именно — Британия, если верить Галковскому) посчитал разумным свернуть конфликт со Штатами и перейти в режим «мирного сосуществования».
Можно предположить, что появление этой третьей силы мы должны считать по сути определяющим в мировой политике уже с того момента, когда СССР начал активную «борьбу за мир во всем мире», за разоружение и вообще — когда у коммунистов начали шататься и выпадать зубы.

Гипотеза: всякий период устойчивого мирного сосуществования в любой политической системе есть ни что иное как период равновесия трех сил.

Естественно, о «мире» здесь можно говорить только в ироническом, переносном смысле. Политика есть область войны; конфликт является её душой и стихией. Но священное число три накладывает свой отпечаток даже на эту буйную стихию. Впрочем, в глазах толпы мир есть мир, и он в любом случае лучше войны.

В приложении к внутренней политике можно опять-таки выдвинуть гипотезу, что грамотно организованная политическая система для того, чтобы быть устойчивой, должна включать в себя опять-таки не менее трех элементов. Примеров тому можно привести много — для начала вспомним о Британском парламенте, который состоит именно из трех обязательных элементов: Короля/Королевы, палаты Лордов, палаты общин. И решение парламента вполне легитимно при взаимном утверждении всеми тремя элементами одновременно.

В практическом применении к политологии всё вышесказанное можно свести к простому и практически весьма полезному «правилу треугольника»:

(Правило треугольника) всякое обострение конфликта между двумя сторонами есть удачная интервенция третьей стороны.

Пример применения правила треугольника — моя предыдущая заметка и следующая заметка.

Моя физическая интуиция подсказывает, что данное правило столь же продуктивно, как неустанно пропагандируемая мною «формула Макиавелли». Именно по этой «формуле» я вычислил, кто стоял за Февральским переворотом 1917 года в России. Напомню: в любой политической системе все основные конфликты сводится к конфликту между меньшинством, стоящим у власти, и меньшинством, идущим к власти. Уважаемый schegloff неустанно требует от меня, чтобы я подчеркивал, что это «формула» «Макиавелли» на самом деле не формула и не Макиавелли. Он даже шуточно грозился назвать её «формулой Паламана», но это было бы несправедливо, так как в действительности её придумали какие-то современные американские макиавеллианцы — schegloff-у даже удалось найти в Сети ссылку на их труды (естественно, на английском). Но я издавна отношусь к авторским правам и к вопросам приоритета с совершенно безжалостным равнодушием. Идеи не принадлежат и не должны принадлежать никому, но быть общим достоянием всех, кто способен их усвоить.

Если применить «правило треугольника» к развивающемуся на наших глазах конфликту вокруг Украины, то мы должны заключить, что если за конфликтом между Россией и Украиной в действительности стоят внутренние разборки англосаксов (Штаты vs Британия), то виновником обострения ситуации на Украине (Майдан) является ни кто иной как Евросоюз.

Сказанного достаточно, мне остается лишь отослать читателя, пока не знакомого с соображениями Богемика по этому поводу, к его замечательной заметке «Правила королевского крокета». Там сказано всё то, что не сказал я, и благоразумно не сказано как раз то, что сказал я.

PS: Применение «правила треугольника» в психотерапии: Треугольник Карпмана. Благодарю Egde Process за наводку.
PPS: см. также «Закон третьего радующегося»

Сумма двух векторов. Законы сложения векторов. Сумма нескольких векторов. Правило параллелограмма. Вычитание векторов 9

Тема 24.

Сумма векторов. Разность векторов.

Рассмотрим пример. Пусть материальная точка переместилась из точки A в точку B, а затем из точки B в точку C. В результате этих перемещений, которые можно представить векторами AB⃗ и BC⃗, материальная точка переместилась из точки A в точку C. Поэтому результирующее перемещение можно представить вектором AC⃗. Поскольку перемещение из точки A в точку C складывается из перемещения из A в B и перемещения из B в C, то вектор AC⃗ естественно назвать суммой векторов AB⃗ и BC⃗:AC⃗=AB⃗+BC⃗.

Рассмотренный пример приводит нас к понятию суммы двух векторов.

Пусть a⃗ и b⃗ – два вектора. Отметим произвольную точку

A и отложим от этой точки вектор AB⃗ равный a⃗. Затем от точки B отложим вектор BC⃗, равный b⃗. Вектор AC⃗ называется суммой векторов a⃗ и b⃗. Это правило сложения векторов называется правилом треугольника. Рисунок это поясняет.

Сумма векторовa⃗ и b⃗ обозначается так: a⃗+b⃗.

Складывая по правилу треугольника произвольный вектор a⃗ с нулевым вектором, получаем, что для любого вектора a⃗ справедливо равенство

a⃗+0⃗=a⃗

Правило треугольника можно сформулировать также следующим образом: если A, B и C – произвольные точки, то AB⃗+BC⃗=AC⃗.

Это равенство справедливо для произвольных точек A, B и C, в частности, в том случае, когда две из них или даже все три совпадают.

Теорема

Для любых векторов a⃗,b⃗ и c⃗ справедливы равенства:

1. a⃗+b⃗=b⃗+a⃗ (переместительный закон).

2. a⃗+b⃗+c⃗=a⃗+b⃗+c⃗ (сочетательный закон).

Докажем первое равенство. Рассмотрим случай, когда векторы a⃗ и b⃗ не коллинеарны. От произвольной точки A отложим векторы ABAD и на этих векторах построим параллелограмм ABCD. По правилу треугольника AC⃗=AB⃗+BC⃗=a⃗+b⃗. Аналогично AC⃗=AD⃗+DC⃗=b⃗+a⃗. Отсюда следует, что a⃗+b⃗=b⃗+a⃗.

При доказательстве первого свойства мы обосновали так называемое правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы a⃗ и b⃗, нужно отложить от какой-нибудь точки A векторы AB⃗=a⃗ и AD⃗=b⃗ и построить параллелограмм ABCD. Тогда вектор AC⃗ равен a⃗+b⃗. Правило параллелограмма часто используется в физике, например при сложении двух сил.

Сложение нескольких векторов производится следующим образом: первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т.д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются. Например, от произвольной точки A отложен вектор AB⃗=a⃗, затем от точки B отложен вектор BC⃗=b⃗ и, наконец, от точки С отложен вектор CD⃗=c⃗. В результате получается вектор AD⃗=a⃗+b⃗+c⃗.

Аналогично можно построить сумму четырех, пяти и вообще любого числа векторов. Это правило построения суммы нескольких векторов называется правилом многоугольника.

Разностью векторов a⃗ и b⃗ называется такой вектор, сумма которого с вектором b⃗ равна вектору a⃗.

Разность векторов a⃗ и b⃗ обозначается так:a⃗-b⃗.

Рассмотрим задачу о построении двух векторов.

Даны векторы a⃗ и b⃗. Построить вектор a⃗-b⃗.

Отметим на плоскости произвольную точку O и отложим от этой точки векторы OA⃗=a⃗ и OB⃗=b⃗.

По правилу треугольника OB⃗+BA⃗=OA⃗ или b⃗+BA⃗=a⃗. Таким образом, сумма векторов BA⃗ и b⃗ равна a⃗. По определению разности векторов это означает, что BA⃗=a⃗-b⃗, то есть вектор BA⃗ искомый.

Пусть a⃗ – произвольный ненулевой вектор. Вектор a1⃗ называется противоположным вектору a⃗, если векторы a⃗ и a1⃗ имеют равные длины и противоположно направлены.

Вектор, противоположный вектору a⃗, обозначается так: -a⃗. Очевидно, что a⃗+-a⃗=0⃗.

Теорема

Для любых векторов a⃗ и b⃗ справедливо равенство a⃗-b⃗=a⃗+-b⃗.

Сегодня мы научились складывать и вычитать векторы. Узнали правило треугольника, правило параллелограмма и правило многоугольника.

сторон треугольника — формула, свойства, правило, примеры

стороны треугольника — это прямые линии, которые соединяются тремя вершинами треугольника. Другими словами, мы можем сказать, что стороны треугольника — это отрезки, пересекающиеся в вершинах треугольника. Стороны прямоугольного треугольника можно найти с помощью различных методов, таких как теорема Пифагора или с помощью периметра треугольника. В случае, если некоторые углы и другие длины сторон заданы, мы можем использовать закон косинусов или закон синусов, чтобы найти длины сторон треугольника.

В этой статье мы рассмотрим понятие сторон треугольника и его формулу. Мы также обсудим свойства и правила сторон треугольника и решим несколько примеров, основанных на концепции, для лучшего понимания.

1.	Каковы стороны треугольника?
2.	Стороны треугольника Формула
3.	Стороны треугольника Свойства
4.	Стороны треугольника Правило
5.	Часто задаваемые вопросы о сторонах треугольника

Каковы стороны треугольника?

У каждого треугольника три стороны и три угла. Эти стороны треугольника представляют собой отрезки прямой линии, так что две стороны встречаются в каждой вершине треугольника, образуя трехстороннюю замкнутую фигуру. В прямоугольном треугольнике каждая сторона имеет имя. Самая длинная сторона прямоугольного треугольника называется гипотенузой, меньшая сторона треугольника называется основанием, а линия стояния, примыкающая к прямому углу, называется перпендикуляром. На концах каждой стороны треугольника, то есть в каждой вершине, образованы три угла. Теперь обсудим формулу, используемую для нахождения длин этих сторон.

Стороны треугольника Формула

Стороны треугольника. Формула данного треугольника для нахождения его сторон связана с тригонометрическими отношениями. К необходимым условиям относятся — одна сторона треугольника и острый угол и таким образом, мы можем узнать остальные стороны треугольника.

• В случае прямоугольного треугольника мы можем напрямую применить теорему Пифагора.
• В случае равнобедренного треугольника мы можем использовать формулу площади или периметра.
• В случае общего, некоторые из углов и некоторые длины сторон известны, мы можем использовать закон косинусов или закон синусов.

Формула сторон треугольника

1. Если нам известны угол и длина стороны прямоугольного треугольника,

• Синус θ = длина противоположной стороны / длина стороны гипотенузы
• Cos θ = длина прилегающей стороны / длина стороны гипотенузы
• Tan θ = длина противоположной стороны / длина соседней стороны

2. Закон синусов: sin(A)/a = sin(B)/b = sin(C)/c

Где,

• a, b и c — стороны противоположных треугольников.
• A, B и C — соответствующие углы.

3. Закон косинусов: c ² = a ² + b ² — 2ab cos(C)

Где

• a, b, c — стороны треугольника с.
• °С — угол, образованный сторонами а и b.

Используем приведенные выше формулы для нахождения длины сторон треугольника в зависимости от известных величин треугольника.

Свойства сторон треугольника

Теперь, когда мы обсудили формулы для нахождения длин сторон треугольника, давайте рассмотрим некоторые важные свойства сторон треугольника:

• Сторона, противоположная наибольшему углу треугольника, равна самая длинная сторона треугольника.
• Два треугольника называются конгруэнтными, если длины соответствующих сторон треугольника равны.
• Два треугольника называются подобными, если длины соответствующих сторон треугольника пропорциональны.
• Сумма трех сторон треугольника дает периметр треугольника.
• Площадь треугольника можно рассчитать, используя три стороны треугольника (формула Герона), формула которой:
  • Площадь = √[s(s – a)(s – b)(s – c)], где a, b, c – три стороны треугольника, а s – полупериметр.

Стороны треугольника Правило

До сих пор мы обсуждали важные свойства сторон треугольника, теперь давайте разберемся с его основным правилом. Правило сторон треугольника состоит в том, что сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Это правило также известно как теорема о неравенстве треугольника. Отсюда следует, что у нас не может быть треугольника с длинами 3, 4, 9.как 3 + 4 = 7 < 9. Давайте посмотрим на применение сторон формулы и правила треугольника в следующем разделе.

Важные примечания о сторонах треугольника

• Стороны треугольника представляют собой прямые линии, которые соединяются тремя вершинами треугольника.
• В случае прямоугольного треугольника мы можем применить теорему Пифагора или формулу тригонометрических соотношений, чтобы найти стороны.
• Мы можем использовать закон косинусов или закон синусов, чтобы найти длины сторон треугольника.

☛ Статьи по теме:

• Типы треугольников
• Построение треугольников
• Подобные треугольники

 

1. Пример 1: Каковы стороны прямоугольного треугольника, гипотенуза которого равна 10 дюймам, а угол при основании равен 30°?

   Решение: Найти: Стороны прямоугольного парка.

   Дано,

   Гипотенуза = 10 дюймов

   Угол при основании = 30 градусов

   Используя формулу сторон треугольника,

   sin θ = длина противоположной стороны / длина стороны гипотенузы

   ⇒ sin 30° = x/10 — (Предположим, что длина противоположной стороны = x)

   ⇒ 1/2 = x/10

   ⇒ x = 5 в

   И, cos θ = длина смежной стороны / длина стороны гипотенузы

   ⇒ cos 30°= y/10 — ( Предположим, что длина смежной стороны = y)

   ⇒ √3/2 = y/10

   ⇒ y = 5√3 в

   Ответ: Остальные стороны треугольного парка равны 5 дюймам и 5√3 дюймам.

2. Пример 2: Длины двух сторон треугольника ABC равны 10 единицам и 9 единицам, а угол между ними равен 47°. Найдите длину третьей стороны треугольника.

   Решение: Чтобы найти длину третьей стороны треугольника, воспользуемся законом косинусов.

   Имеем a = 10, b = 9 и угол C = 47°. Нам нужно найти значение c. Итак, у нас

   c ² = a ² + b ² — 2ab cos(C)

   ⇒ c ² = 10 ² + 9 90 087 2 — 2 × 10 × 9 cos(47°)

   = 100 + 81 — 180 × 0,682

   = 58,24

   ⇒ с = √58,24

   = 7,63 ед.

   Ответ: Длина третьей стороны треугольника равна 7,63 единицы.

3. Пример 3: В треугольнике ABC ∠C = 42° и ∠A = 33°, а сторона, противоположная углу C, равна 12,5 единицы. Найдите длину стороны треугольника, противоположной углу А.

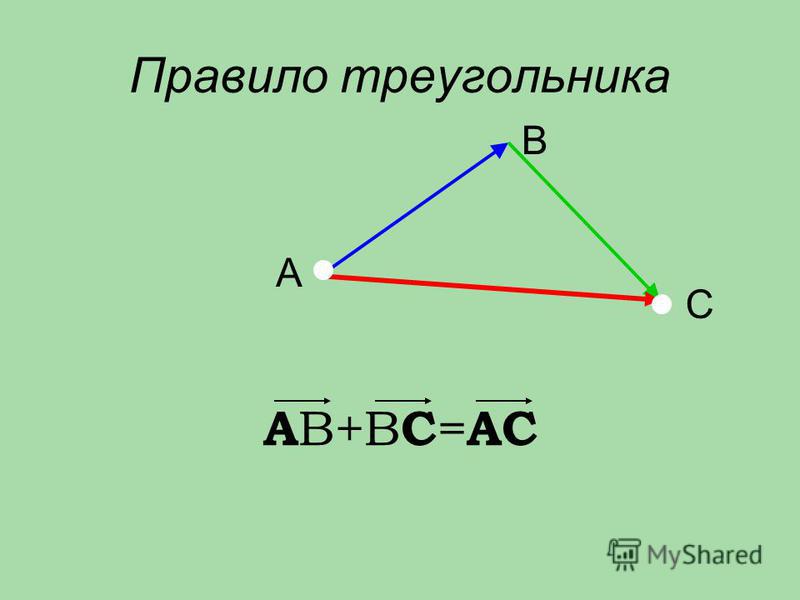
   Решение: Имеем ∠C = 42° и ∠A = 33°, c = 12,5 единиц. Нам нужно найти сторону «а». Таким образом, используя Закон синуса, мы имеем

   SINA / A = SINC / C

   ⇒ SIN (33 °) / A = SIN (42 °) / 12,5

   ⇒ 0,545 / A = 0,67 / 12,5

   ⇒ A = 12,5 × 0,545 ÷ 0,67

   = 10,17 ед.

   Ответ: Длина стороны, противоположной углу А, равна 10,17 ед.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных эффектов.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Стороны треугольника Вопросы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о сторонах треугольника

Какие стороны треугольника в геометрии?

Стороны треугольника представляют собой отрезки прямой линии, две стороны которых сходятся в каждой вершине треугольника, образуя трехстороннюю замкнутую фигуру.

Формула определения сторон треугольника?

Чтобы найти стороны треугольника, мы используем различные формулы в зависимости от известных значений для данного треугольника. Мы используем закон косинусов или закон синусов, если даны некоторые стороны и некоторые углы. Мы можем использовать теорему Пифагора, чтобы найти стороны прямоугольного треугольника. Мы также можем использовать формулу тригонометрического отношения в случае прямоугольного треугольника.

Когда использовать формулы сторон треугольника?

Мы можем использовать формулу тригонометрических соотношений или формулу теоремы Пифагора только в случае прямоугольного треугольника, так как она включает в себя тригонометрические соотношения, применяемые для нахождения сторон данного треугольника. В случае, если некоторые углы и другие длины сторон заданы, мы можем использовать закон косинусов или закон синусов.

Как использовать формулы сторон треугольника?

Если нам дан угол и длина стороны треугольника,

• Шаг 1: Проверка типа треугольника.
• Шаг 2. Проверьте наличие известных сторон или углов.
• Шаг 3: Поместите данные значения в стороны треугольника по формуле: Синус θ = длина противоположной стороны / длина стороны гипотенузы, Cos θ = длина прилежащей стороны / длина стороны гипотенузы, Tan θ = длина противоположной стороны / Длина смежной стороны или напрямую использовать закон синуса или закон косинуса соответственно.

Каково применение сторон формулы треугольника?

Формула для сторон треугольника имеет приложения в тригонометрии, которая также имеет множество применений в нашей повседневной жизни, от создания карт до строительства зданий.

Каковы важные свойства сторон треугольника?

Некоторые важные свойства сторон треугольника:

• Сторона, противоположная наибольшему углу треугольника, является самой длинной стороной треугольника.
• Два треугольника называются конгруэнтными, если длины соответствующих сторон треугольника равны.
• Два треугольника называются подобными, если длины соответствующих сторон треугольника пропорциональны.
• Сумма трех сторон треугольника дает периметр треугольника.

Правило сторон треугольника?

Правило сторон треугольника состоит в том, что сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Это правило также известно как теорема о неравенстве треугольника.

Каковы 3 стороны прямоугольного треугольника?

Три стороны прямоугольного треугольника — это Гипотенуза (самая длинная сторона), Перпендикуляр (также называемая противоположной стороной) и Основание (также называемая прилежащей стороной).

Как найти стороны треугольника с углами?

Чтобы найти длину стороны треугольника с углами, нам нужна хотя бы одна сторона. Затем мы можем использовать закон синусов, чтобы найти длину сторон треугольника.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист сторон треугольника

Правила определения длины сторон треугольника

••• Thinkstock/Comstock/Getty Images

Обновлено 24 апреля 2017 г.

Автор Sreela Datta

Euc лидова геометрия, базовая геометрия, преподаваемая в школе, требует определенных соотношений между длинами сторон треугольника. Нельзя просто взять три случайных отрезка и составить треугольник. Отрезки должны удовлетворять теоремам о неравенстве треугольника. Другими теоремами, определяющими отношения между сторонами треугольника, являются теорема Пифагора и закон косинусов.

Первая теорема о неравенстве треугольника

Согласно первой теореме о неравенстве треугольника, сумма длин любых двух сторон треугольника должна быть больше, чем длина третьей стороны. Это означает, что вы не можете нарисовать треугольник со сторонами, например, 2, 7 и 12, поскольку 2 + 7 меньше 12. Чтобы получить интуитивное представление об этом, представьте, что вы сначала рисуете отрезок длиной 12 см. Теперь подумайте о двух других отрезках длиной 2 см и 7 см, прикрепленных к двум концам отрезка длиной 12 см. Ясно, что свести два концевых отрезка было бы невозможно.