Что такое асимметрия и симметрия в искусстве?
И в искусстве, и в природе присутствуют такие понятия, как симметрия и асимметрия. Их мы наблюдаем повседневно в окружающем нас мире. И каждому субъекту присущи одно из или оба этих понятия.
Что такое асимметрия в искусстве
Это полная противоположность симметрии. В искусстве она помогает выразить динамичность действия, показать естественность и непринужденность движения, разнообразить композицию.
В асимметричной композиции симметрия либо слегка нарушена, либо отсутствует полностью. Предметы могут быть расположены в одной части холста и нести там большую нагрузку. Вот что такое асимметрия. При этом гармоничность в асимметричной композиции не нарушается, но при условии, что художник подчиняется определенным правилам ее построения.
Асимметрию мы можем наблюдать в естественной природе. Человеческое тело, например, не абсолютно симметрично. Конечности могут незначительно отличаться по длине или толщине, одна половина лица отличается от другой изгибом губ, морщинок, расположением бровей и другим. На фото ниже наглядно видно, что такое асимметрия. Согласитесь, если бы наши черты лица были симметричными, это выглядело бы не очень привлекательно!

Симметрия в жизни
Многим объектам свойственна симметрия. Она подразумевает, что определенные части имеют равновесие относительно центральной оси или точки.

Если предмет делится на равные части и его крайние точки одной стороны повторяют такие же противоположной, то о нем можно судить как о симметричном. Большое внимание симметрии уделяют перфекционисты.
Она применяется в декоративном искусстве (в рисовании орнаментов, например). Симметрия и асимметрия в композиции часто используются. Например, художники в эпоху Возрождения воспринимали язык симметрии как отображение идеального, уравновешенного состояния того или иного объекта. Они стремились воплотить в жизнь ее законы.
Применение симметрии и асимметрии в искусстве
В картине «Обручение девы Марии» художника Возрождения Рафаэля Санти мир отображен в полной гармонии и всем своем великолепии. В каждом объекте заключена строгая логика.
 Что такое асимметрия для картин? В работе Рафаэля создается впечатление торжественности, но вместе с тем персонажи отстранены от зрителя, они погружены в свои раздумья, и одновременно хорошо выражается их динамика, которая свойственна асимметрии. Ведь только с помощью нее можно хорошо выразить действия.
Что такое асимметрия для картин? В работе Рафаэля создается впечатление торжественности, но вместе с тем персонажи отстранены от зрителя, они погружены в свои раздумья, и одновременно хорошо выражается их динамика, которая свойственна асимметрии. Ведь только с помощью нее можно хорошо выразить действия.Главное действие, надевание обручального кольца на палец Марии, заключено в самый центр композиции. Симметрично располагается на картине храм на заднем фоне, в самом центре. Таким образом, зритель сразу может определить главные действия на картине, соотнести их и понять, в чем заключается смысл.
Некоторые фигуры композиции все же нарушают симметрию, располагаясь вне определенной последовательности. Таким образом, симметрия и асимметрия в композиции помогают выделить главные действия и вместе создают гармоничную работу.
|
АСИММЕТРИЯ
Асимметрия по структуре своей противоположна явлению симметрии. Если композиция построена асимметрично, то она, как правило, не симметрична, и, наоборот, если композиция симметрична, то она, как правило, не асимметрична. Это вполне доказывает, что симметрия и асимметрия являются взаимно обусловленными правилами композиции. Как художественный приём, асимметрия придаёт динамику, разнообразие произведению искусства (например, барокко, рококо, романтизме), вносит элементы непринуждённости, естественной случайности (импрессионизм), гротескность, причудливость (модерн). В архитектуре асимметричность может обуславливаться функциональным назначением зданий. В асимметричной композиции равновесие достигается введением пространственных пауз между предметами, которые при этом либо приближаются друг к другу, либо отдаляются. Равновесие достигается и через противопоставление больших и малых форм, контрастов темного и светлого, яркого и приглушенного по цвету. В асимметричной децентрализованной композиции иногда равновесие сознательно ослабляется или даже совсем отсутствует, например в тех случаях, когда смысловой центр находится ближе к одной из сторон композиции, а другая ее часть менее загружена. Если сюжет раскрывается через контрасты положений, контрасты социальные и психологические, характеризующие главного героя или группировки фигур, расположенных друг от друга на расстоянии, то внешне кажется, что они расчленяют композицию по принципу симметрии. На самом же деле двучастное противопоставление образует единство противоположностей, которое придает равновесие композиции. Асимметричной композиции ближе ощущение движения, беспокойства. В такой композиции составляющие части относительно центральной оси неодинаковые. Но главная задача остается прежней — сохранить равновесие путем подбора и расположения элементов в пространстве картины и в определенных пропорциях по форме, тону, цвету. Равновесие достигается и с изменением пространственных пауз между фигурами. Примерами асимметричного построения с достижением равновесия композиции могут служить такие полотна, как «Последний день Помпеи» К. П. Брюллова, «На старом уральском заводе» Б. В. Иогансона, «Раздолье» А. А. Дейнеки и многие, многие другие. На картине «Раздолье» изображены девушки-спортсменки, бегущие снизу, от реки, вверх, по крутому высокому берегу. На втором и дальних планах открываются широкие дали пейзажа средней полосы России. Стремительный порыв, объединяющий бегущих девушек, создает впечатление ритма и динамичности композиции. Степень интенсивности движения нарастает из глубины и наиболее активно проявляется на переднем плане. Бесспорно, что композиция не симметричная. Чередование же светлых фигур с элементами пейзажа уравновешивает динамичную композицию, воспринимаемую цельным и ритмичным произведением. |
22 вдохновляющих примера использования асимметрии в интерьере
Наверх Перепланировки- Каталог домов
- Квартира
- Спальня
- Кухня
- Столовая
- Гостиная
- Ванная комната, санузел
- Прихожая
- Детская
- Мансарда
- Маленькие комнаты
- Рабочее место
- Гардеробная
- Библиотека
- Декорирование
- Мебель
- Аксессуары
- Загородный дом
- Ландшафт
- Системы хранения
- Коридор
- Уборка
- Фундамент
- Кровля
- Стены
- Двери и перегородки
- Потолок
- Балконы и лоджии
- Внутренние конструкции
- Пол
- Водоснабжение и канали
Симметрия — Википедия
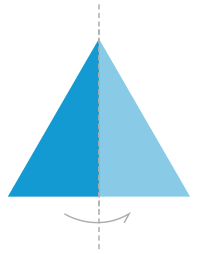 Равнобедренный треугольник с зеркальной симметрией. Пунктирная линия является осью симметрии
Равнобедренный треугольник с зеркальной симметрией. Пунктирная линия является осью симметрии  Рисунок бабочки с двусторонней симметрией
Рисунок бабочки с двусторонней симметрией(др.-греч. συμμετρία = «соразмерность»; от συμ- «совместно» + μετρέω «мерю»), в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях (например: положения, энергии, информации, другого). Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя центр на месте и если поверхность тела однородна). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.
Симметрия — основополагающий принцип самоорганизации материальных форм в природе и формообразования в искусстве[1]. Отсутствие или нарушение симметрии называется асимметрией или диссимметрией[2].
Общие симметрийные свойства описываются с помощью теории групп.
Симметрии могут быть точными или приближёнными.
 Два треугольника с точечной симметрией отражения в плоскости. Треугольник А’В’С может быть получен из треугольника ABC поворотом на 180 ° вокруг точки O.
Два треугольника с точечной симметрией отражения в плоскости. Треугольник А’В’С может быть получен из треугольника ABC поворотом на 180 ° вокруг точки O. 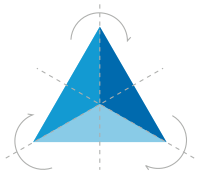
Геометрическая симметрия — это наиболее известный тип симметрии для многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг, повёрнутый вокруг своего центра, будет иметь ту же форму и размер, что и исходный круг. Поэтому круг называется симметричным относительно вращения (имеет осевую симметрию). Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования.
Виды геометрических симметрий:
Зеркальная симметрия[править | править код]
Зеркальная симметрия или отражение— движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью). Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, то есть, когда объект при операции отражения переходит в себя. Это математическое понятие в оптике описывает соотношение объектов и их (мнимых) изображений при отражении в плоском зеркале. Проявляется во многих законах природы (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении).
Осевая симметрия[править | править код]
Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.
Вращательная симметрия[править | править код]
Вращательная симметрия — термин, означающий симметрию объекта относительно всех или некоторых собственных вращений m-мерного евклидова пространства. Собственными вращениями называются разновидности изометрии, сохраняющие ориентацию. Таким образом, группа симметрии, отвечающая вращениям, есть подгруппа группы E
Трансляционная симметрия может рассматриваться как частный случай вращательной — вращение вокруг бесконечно-удалённой точки. При таком обобщении группа вращательной симметрии совпадает с полной E+(m). Такого рода симметрия неприменима к конечным объектам, поскольку делает всё пространство однородным, однако она используется в формулировке физических закономерностей.
Совокупность собственных вращений вокруг фиксированной точки пространства образуют специальную ортогональную группу SO(m) — группу ортогональных матриц m×m с определителем, равным 1. Для частного случая m = 3 группа носит специальное название — группа вращений.
В физике инвариантность относительно группы вращений называется изотропностью пространства (все направления в пространстве равноправны) и выражается в инвариантности физических законов, в частности, уравнений движения, относительно вращений. Теорема Нётер связывает эту инвариантность с наличием сохраняющейся величины (интеграла движения) — углового момента.
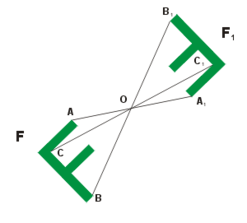 Центральная симметрия
Центральная симметрияСимметрия относительно точки[править | править код]
Центра́льной симме́трией (иногда центра́льной инве́рсией) относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA{\displaystyle Z_{A}}, в то время как обозначение SA{\displaystyle S_{A}} можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Другие названия этого преобразования —
Скользящая симметрия[править | править код]
Скользящая симметрия — изометрия евклидовой плоскости. Скользящей симметрией называют композицию симметрии относительно некоторой прямой l{\displaystyle l} и переноса на вектор, параллельный l{\displaystyle l} (этот вектор может быть и нулевым). Скользящую симметрию можно представить в виде композиции 3 осевых симметрий (теорема Шаля).
В теоретической физике поведение физической системы описывается некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения). Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.
Суперсимметрия[править | править код]
Суперсимме́трия или симме́трия Ферми́ — Бозе́ — гипотетическая симметрия, связывающая бозоны и фермионы в природе. Абстрактное преобразование суперсимметрии связывает бозонное и фермионное квантовые поля, так что они могут превращаться друг в друга. Образно можно сказать, что преобразование суперсимметрии может переводить вещество во взаимодействие (или в излучение), и наоборот.
По состоянию на начало 2009 года суперсимметрия является физической гипотезой, не подтверждённой экспериментально. Совершенно точно установлено, что наш мир не является суперсимметричным в смысле точной симметрии, так как в любой суперсимметричной модели фермионы и бозоны, связанные суперсимметричным преобразованием, должны обладать одинаковыми массой, зарядом и другими квантовыми числами (за исключением спина). Данное требование не выполняется для известных в природе частиц. Предполагается, тем не менее, что существует энергетический лимит, за пределами которого поля подчиняются суперсимметричным преобразованиям, а в рамках лимита — нет. В таком случае частицы-суперпартнёры обычных частиц оказываются очень тяжёлыми по сравнению с обычными частицами. Поиск суперпартнёров обычных частиц — одна из основных задач современной физики высоких энергий. Ожидается, что Большой адронный коллайдер[3] сможет открыть и исследовать суперсимметричные частицы, если они существуют, или поставить под большое сомнение суперсимметричные теории, если ничего не будет обнаружено.
Трансляционная симметрия[править | править код]
Трансляционная симметрия — тип симметрии, при которой свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Например, однородная среда совмещается сама с собой при сдвиге на любой вектор, поэтому для неё свойственна трансляционная симметрия.
Трансляционная симметрия свойственна также для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число. Среди всех векторов трансляций кристаллической решётки можно выбрать 3 линейно независимых таким образом, что любой другой вектор трансляции был бы целочисленно-линейной комбинацией этих трёх векторов. Эти три вектора составляют базис кристаллической решётки.
Теория групп показывает, что трансляционная симметрия в кристаллах совместима только с поворотами на углы θ=2π/n, где n может принимать значения 1, 2, 3, 4, 6.
При повороте на углы 180, 120, 90, 60 градусов положение атомов в кристалле не меняется. Говорят, что кристаллы имеют ось вращения n-го порядка.[уточнить]
Перенос в плоском четырёхмерном пространстве-времени не меняет физических законов. В теории поля трансляционная симметрии, согласно теореме Нётер, соответствует сохранению тензора энергии-импульса. В частности, чисто временные трансляции соответствуют закону сохранения энергии, а чисто пространственные сдвиги — закону сохранения импульса.
Сложные узоры на крыльях бабочки являются одним из примеров двусторонней симметрииСимметрия в биологии — это закономерное расположение подобных (одинаковых, равных по размеру) частей тела или форм живого организма, совокупности живых организмов относительно центра или оси симметрии. Тип симметрии определяет не только общее строение тела, но и возможность развития систем органов животного. Строение тела многих многоклеточных организмов отражает определённые формы симметрии. Если тело животного можно мысленно разделить на две половины, правую и левую, то такую форму симметрии называют билатеральной. Этот тип симметрии свойственен подавляющему большинству видов, а также человеку. Если тело животного можно мысленно разделить не одной, а несколькими плоскостями симметрии на равные части, то такое животное называют радиально-симметричным. Этот тип симметрии встречается значительно реже.
Асимметрия — отсутствие симметрии. Иногда этот термин используется для описания организмов, лишённых симметрии первично, в противоположность диссимметрии — вторичной утрате симметрии или отдельных её элементов.
Понятия симметрии и асимметрии обратны. Чем более симметричен организм, тем менее он асимметричен и наоборот. Небольшое количество организмов полностью асимметричны. При этом следует различать изменчивость формы (например у амёбы) от отсутствия симметрии. В природе и, в частности, в живой природе симметрия не абсолютна и всегда содержит некоторую степень асимметрии. Например, симметричные листья растений при сложении пополам в точности не совпадают.
У биологических объектов встречаются следующие типы симметрии:
Радиальная симметрия[править | править код]
В биологии о радиальной симметрии говорят, когда через трёхмерное существо проходят одна или более осей симметрии. При этом радиальносимметричные животные могут и не иметь плоскостей симметрии. Так, у сифонофоры Velella имеется ось симметрии второго порядка и нет плоскостей симметрии[4]
Обычно через ось симметрии проходят две или более плоскости симметрии. Эти плоскости пересекаются по прямой — оси симметрии. Если животное будет вращаться вокруг этой оси на определённый градус, то оно будет отображаться само на себе (совпадать само с собой). Таких осей симметрии может быть несколько (полиаксонная симметрия) или одна (монаксонная симметрия). Полиаксонная симметрия распространена среди протистов (например, радиолярий).
Как правило, у многоклеточных животных два конца (полюса) единственной оси симметрии неравноценны (например, у медуз на одном полюсе (оральном) находится рот, а на противоположном (аборальном) — верхушка колокола. Такая симметрия (вариант радиальной симметрии) в сравнительной анатомии называется одноосно-гетеропольной. В двухмерной проекции радиальная симметрия может сохраняться, если ось симметрии направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.
Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии. У иглокожих радиальная симметрия вторична: их личинки двустороннесимметричны, а у взрослых животных наружная радиальная симметрия нарушается наличием мадрепоровой пластинки.
Кроме типичной радиальной симметрии существует двулучевая радиальная симметрия (две плоскости симметрии, к примеру, у гребневиков). Если плоскость симметрии только одна, то симметрия билатеральная (такую симметрию имеют животные из группы Bilateria).
У цветковых растений часто встречаются радиальносимметричные цветки: 3 плоскости симметрии (водокрас лягушачий), 4 плоскости симметрии (лапчатка прямая), 5 плоскостей симметрии (колокольчик), 6 плоскостей симметрии (безвременник). Цветки с радиальной симметрией называются актиноморфные, цветки с билатеральной симметрией — зигоморфные.
Билатеральная симметрия[править | править код]
Билатера́льная симме́трия (двусторонняя симметрия) — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны. Если на плоскость симметрии опустить перпендикуляр из точки A и затем из точки О на плоскости симметрии продолжить его на длину AО, то он попадёт в точку A1, во всём подобную точке A. Ось симметрии у билатерально симметричных объектов отсутствует. У животных билатеральная симметрия проявляется в схожести или почти полной идентичности левой и правой половин тела. При этом всегда существуют случайные отклонения от симметрии (например, различия в папиллярных линиях, ветвлении сосудов и расположении родинок на правой и левой руках человека). Часто существуют небольшие, но закономерные различия во внешнем строении (например, более развитая мускулатура правой руки у праворуких людей) и более существенные различия между правой и левой половиной тела в расположении внутренних органов. Например, сердце у млекопитающих обычно размещено несимметрично, со смещением влево.
У животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих.
Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых форм трипаносом, бодонид, раковинок многих фораминифер. У растений билатеральную симметрию имеет обычно не весь организм, а его отдельные части — листья или цветки. Билатерально симметричные цветки ботаники называют зигоморфными.
Симметрия важна для химии, так как она объясняет наблюдения в спектроскопии, квантовой химии и кристаллографии.
Кристаллографическая точечная группа симметрии — это точечная группа симметрии, которая описывает макросимметрию кристалла. Поскольку в кристаллах допустимы оси (поворотные и несобственного вращения) только 1, 2, 3, 4 и 6 порядков, из всего бесконечного числа точечных групп симметрии только 32 относятся к кристаллографическим.
Анизотропия (от др.-греч. ἄνισος — неравный и τρόπος — направление) — различие свойств среды (например, физических: упругости, электропроводности, теплопроводности, показателя преломления, скорости звука или света и др.) в различных направлениях внутри этой среды; в противоположность изотропии. Причиной анизотропности кристаллов является то, что при упорядоченном расположении атомов, молекул или ионов силы взаимодействия между ними и межатомные расстояния (а также некоторые не связанные с ними прямо величины, например, поляризуемость или электропроводность) оказываются неодинаковыми по различным направлениям. Причиной анизотропии молекулярного кристалла может быть также асимметрия его молекул. Макроскопически эта неодинаковость проявляется, как правило, лишь если кристаллическая структура не слишком симметрична.

Предполагается, что тенденция людей видеть цель в симметрии, является одной из причин, почему симметрия часто является неотъемлемой частью символов мировых религий. Вот лишь некоторые из многих примеров, изображённые на рисунке справа.
Люди наблюдают симметричную природу (также включающую асимметричный баланс) социального взаимодействия в различных контекстах. Они включают оценки взаимности, эмпатии, извинения, диалога, уважения, справедливости и мести. Симметричные взаимодействия посылают сигналы «мы одинаковые», а асимметричные взаимодействия выражают мысль «я особый, лучше, чем ты». Взаимоотношения со сверстниками строятся на основе симметрии, а властные отношения — на асимметрии[5].
Типы симметрий, встречающиеся в математике и в естественных науках:

Краб-скрипач, Uca pugnax

Камбала
Асимметрией (др.-греч. ασυμμετρία «несоразмерность» от μετρέω «измеряю») можно считать любое нарушение симметрии. Чаще всего термин употребляется в отношении зрительных объектов и в изобразительном искусстве. В художественном творчестве асимметрия может выступать (и очень часто выступает) в качестве одного из основных средств формообразования (или композиции). Одно из близких понятий в искусстве — аритмия.
В связи с постоянным делением клеток в организме асимметрия в организмах является обычным явлением по крайней мере в одном измерении наравне с биологической симметрией (также см. Межполушарная асимметрия). Луи Пастер полагал, что биологические молекулы асимметричны из-за космических [то есть физических] сил, которые осуществляют контроль над их формированием, закладывая свойства (асимметричность), аналогичные своим. Хоть и в его время, и даже сейчас, симметрии в физических процессах придаётся большее значение, так же известны фундаментальные физические асимметрии, начиная с времени.
Существует понятие «преобладающая рука», означающее асимметрию в развитии навыков людей и животных. Тренировка нервных путей во время обучения навыку с одной рукой (лапой) занимает меньше времени, чем та же тренировка с двумя.[6]
Понятие асимметрии существует также в физике (Барионная асимметрия Вселенной, Омическая асимметрия, Ёмкостная асимметрия), математике (Коэффициент асимметрии, Асимметричное отношение, Асимметрический атом, Асимметричная криптография) архитектуре и т. д.
- Урманцев Ю. А. Симметрия природы и природа симметрии. — М., Мысль, 1974.
- Вигнер Е. Этюды о симметрии. — М., Мир, 1971. — 320 с.
- Нокс Р., Голд А. Симметрия в твердом теле. — М., Наука, 1970. — 424 с.
- Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. — М., Наука, 1972. — 340 с.
- Вернадский В. И. Химическое строение биосферы Земли и её окружения. — М., Наука, 1965. — 373 с.
- Болтянский В. Г., Виленкин Н. Я. Симметрия в алгебре. — М., Наука, 1967. — 284 с.
- Под ред. Сенешаль М., Флека Дж. Узоры симметрии. — М., Мир, 1980. — 269 с.
- Ю. К. Егоров-Тисменко, Г. П. Литвинская Теория симметрии кристаллов, ГЕОС, 2000.
- П. М. Зоркий Симметрия молекул и кристаллических структур, МГУ, 1986.
- А. В. Шубников Симметрия и антисимметрия конечных фигур, Изд-во АН СССР, 1951
- И. Харгиттаи, М. Харгиттаи Симметрия глазами химика. — М., Мир, 1989. — 494 с.
Конспект урока Симметрия и ассиметрия
6 класс __________________
Тема «Передача симметрии и асимметрии в композиции».
Структура урока:
Вступительное слово учителя (5 минут).
Представление темы в виде презентации (15 минут).
Творческая работа (20 минут).
Подведение итогов.
Оценивание работ учеников (5 минут).
Задачи:
Образовательные: сформировать понятие движения в пространстве, усвоение учащимися понятия «симметрия».
Развивающие: приобретение навыков работы с большими объемами информации;
Совершенствовать память и умение образного сравнения.
Воспитательные: воспитание чувства прекрасного; воспитание творчества.
Цели: построение симметричных и асимметричных композиций;
Развитие пространственного мышления.
Оборудование: презентация, репродукции
Ход урока:
1. Орг.момент. Проверка посещаемости и готовности к уроку.
2. Вступление. Сегодня наш разговор пойдет о построении симметричных и асимметричных композиций. Давайте вспомним такое симметрия и асимметрия. «Симметрия» — греческое слово, и означает в буквальном переводе — соразмерность.
« Асимметрия» — отсутствие соразмерности в композиции.
Асимметрия» — отсутствие соразмерности в композиции.
Симметрию изучают в философии, астрономии, математике, физике, химии, медицине и биологии.
Мы же рассмотрим это понятие с точки зрения ее художественной выразительности.
Симметрия в природе и жизни — это строение цветка, бабочки, орнамента, техники (самолет, вертолет…). Интересна объемная симметрия кристаллов, пространственных моделей атомов, молекул.
В изобразительном и декоративном искусстве симметрия является одним из средств создания гармоничной структуры произведения.
изобразительном и декоративном искусстве симметрия является одним из средств создания гармоничной структуры произведения.
Но в разные исторические периоды отношение симметрии и асимметрии было неоднозначным. Асимметрические композиции часто бывают совершенны, как и симметричные.
Художники разных эпох использовали симметричное построение картины. Симметричными были многие древние мозаики и современные.
Живописцы эпохи Возрождения часто строили свои композиции по законам симметрии. Обратите внимание на знаменитую картину Рафаэля « Сикстинская мадонна».
Сикстинская мадонна».
Эта картина находится в картинной галерее в Дрездене.
Образ Марии — серьезно и печально смотрит она в даль. Ее благородный облик полон душевной чистоты и красоты.
Вот такое построение по законам симметрии позволяет достигнуть впечатления покоя, величественности, особой торжественности и значимости событий.
Люди и предметы.
В симметричной композиции люди или предметы расположены почти зеркально по отношению к центральной оси картины.
С имметрия в искусстве основана на реальной действительности, изобилующей симметрично устроенными формами. Например: симметрично устроены фигуры человека, снежинки и т. д.
имметрия в искусстве основана на реальной действительности, изобилующей симметрично устроенными формами. Например: симметрично устроены фигуры человека, снежинки и т. д.

Васнецовские « Богатыри».
«Добрыня, Илья и Алеша Попович на богатырском выезде- примечают в поле, нет ли где врага, не обижают ли где кого»- так объяснял сам художник содержание своей картины.
К артина особенно близка именно русскому человеку, понятны каждому, кому дорога свобода родной земли, кому близки образы ее защитников.
артина особенно близка именно русскому человеку, понятны каждому, кому дорога свобода родной земли, кому близки образы ее защитников.
Здесь симметричная композиция устойчивая, левая и правая половины уравновешены.
В асимметричной композиции расположение объектов может быть самым разнообразным в зависимости от сюжета и замысла произведения, левая и правая половины неуравновешенны. (Брейгель. Картина с охотниками).
Композицию натюрморта или пейзажа легко представить в виде схемы, на которой ясно видно, симметрично или асимметрично построена композиция.
Волшебные загадки.
Два кольца, два конца,
А посередине- гвоздик.
(Можно ли назвать ножницы симметричной фигурой? Почему?)
Хвост на дворе.
Нос в конуре.
Кто хвост повернет,
Тот и в дом войдет.
(Можно ли назвать ключ асимметричной фигурой? Почему?)
На ромашку у ворот
Опустился вертолет-
Золотистые глаза.
Кто же это?……
(Можно ли назвать стрекозу насекомым, у которого имеется ось симметрии?)
Практическая работа.
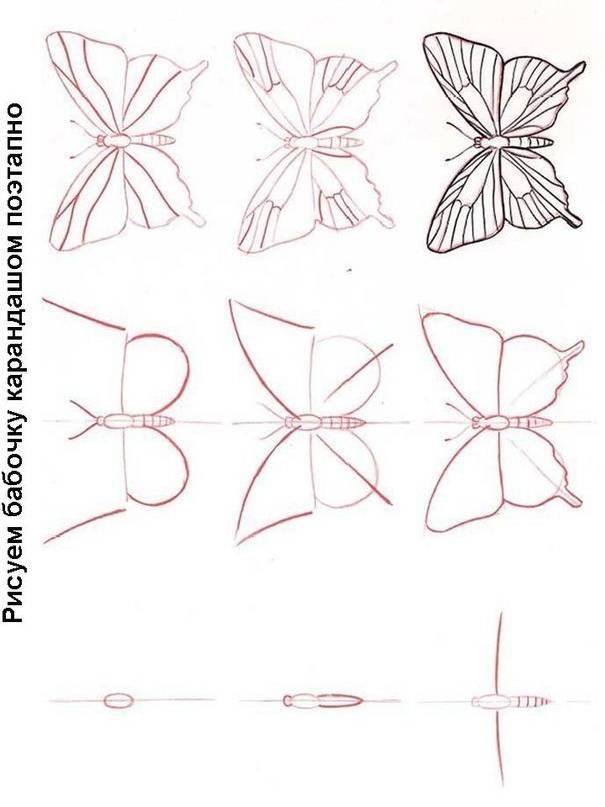
Используя закон композиции симметрию нарисовать бабочку. Свободный выбор цветного материала.
Бабочка расправила крылья – и перед нами разноцветный орнамент из линий и пятен…

Подведение итогов работы, оценка рисунков учащихся.
Д.З.§6 рисунок бабочки дорисовать



Открытый урок по теме «Симметрия — асимметрия»
Цели:
- дать сведения о симметрии-асимметрии, статике и динамике;
- содействовать развитию художественного вкуса, чувство композиции, наблюдательности, верной передачи особенностей натуры;
- активизировать творческое воображение;
- развивать графические умения и навыки в изображении предметов сложной формы, от общего к деталям;
- помогать определению пропорции, формы предмета, его положения в пространстве;
- закрепить знания о композиции, равновесии в композиции;
- формировать умения выражать в рисунке свои зрительные представления;
- воспитать интерес любовь к искусству.
Оборудование:
- альбом,
- карандаш,
- ластик,
- кисти,
- акварель,
- баночка под воду,
- ветошь для кистей.
Зрительный ряд:
Репродукции картин: Леонардо да Винчи “Мадонна в гроте” <Рисунок0>, “Тайная вечеря” <Рисунок1>, Виктор Васнецов “Богатыри” <Рисунок2>, Рафаэль “Сикстинская мадонна” <Рисунок3>, Н. Пуссен “Аркадские пастухи” <Рисунок18>, западный фронтон храма Зевса в Олимпии многофигурная композиция “Борьба лапифов с кентаврами в присутствии бога Апполона” <Рисунок4>, <Рисунок04>, росписи ваз <Рисунок9>, <Рисунок10>, <Рисунок11>, <Рисунок12>.
Рисунки: бабочка <Рисунок5>, олень с ветвистыми рогами <Рисунок6>, лебеди <Рисунок7>, аллея осеннего парка <Рисунок8>, снежинки <Рисунок13>, фигура человека.
Ход урока
1. Организационный момент
2. Основная часть урока
Беседа о “симметрии-асимметрии”
— Бабочка расправила крылья – и перед нами разноцветный орнамент из линий и пятен, могучие рога оленя, разветвляются в стороны, подобны скульптурной композиции, а какое сказочное зрелище – лебеди, отражающиеся в воде, аллея осеннего парка с уходящими вдаль деревьями.
<Рисунок 5>
<Рисунок 6>
<Рисунок 7>
<Рисунок 07>
<Рисунок 8>
<Рисунок 08>
Повсюду можно наблюдать картины, в которых есть одинаковые по форме, тону и цвету, левые и правые стороны, где равновесие наиболее выражено, или, как мы привыкли говорить, стороны симметричны.
— Принцип симметрии может сохраняться и при незначительных отклонениях одной из сторон композиции от центральной оси или при добавлении с любой стороны нескольких деталей /линий, пятен/, изменении насыщенности элементов картины. В природе случаи идеальной геометрической симметрии практически единичны, что нельзя сказать о творениях человеческих рук: произведениях искусства, архитектуре, технике, предметах быта, так называемой второй природе.
— Законам симметрии пользовались еще архитекторы и скульпторы Древней Греции. Ярким выражением его может служить западный фронтон храма Зевса в Олимпии, на котором многофигурная композиция “Борьба лапифов с кентаврами в присутствии бога Аполлона ”, росписи ваз, фресок.
<Рисунок 04>
<Рисунок 4>
<Рисунок 9>
<Рисунок 10>
<Рисунок 11>
<Рисунок 12>
— Скажите, что такое композиция?
— Композиция /от лат./ — составление, соединение, различных частей в единое целое с какой-либо идеей.
— Симметрично построенная композиция встречается во многих произведениях, назовем наиболее известные: “Тайная вечеря”, “Мадонна в гроте” Леонардо да Винчи, “Сикстинская мадонна” Рафаэль, в русском искусстве – “Богатыри” Виктора Васнецова.
<Рисунок 0>
<Рисунок 1>
<Рисунок 3>
<Рисунок 2>
Если симметричная композиция создает впечатление покоя, тишины, торжественности, передает чувство уравновешенности, то асимметричной композиции ближе ощущение движения, беспокойства. В такой композиции составляющие части относительно центральной оси неодинаковые.
— В симметричной композиции люди или предметы расположены почти зеркально по отношению к центральной оси картины. <Рисунок 7>
Симметрия в искусстве усвоена на реальной действительности изобилующей симметрично устроенными формами, например, симметрично устроены фигуры человека, бабочки, снежинки и т.д.
<Рисунок 5>
<Рисунок 13>
<Рисунок 013>
— В асимметричной композиции расположение объектов может быть самым разнообразным в зависимости от сюжета и замысла произведения, левая и правая половины неуравновешенны.
Используя закон симметрии, попробуем передать в эскизах состояние покоя, устойчивости форм одной или несколько фигур.
— Но главная задача – сохранить равновесие путем подбора и расположения элементов в пространстве картины и в определениях пропорциях по форме, тону, цвету.
— При составлении соблюдайте одно условие: элементы композиции расположить ровно, без особого отклонения от вертикали либо горизонтали.
Тогда получим работу, в которой, кроме симметрии, выражено состояние статики.
Симметричные композиции – статичные /устойчивые/, левая и правая половина уравновешены.
<Рисунок 2>
<Рисунок 18>
— Теперь незаметно подошли к другому закону – статике.
— Статика – это покой, устойчивость.
— Статику можно встретить в произведениях искусства в таких как пейзаж, портрет, натюрморт.
— Если формы, линий устремлены в одном направлении, то зрительно создается как бы “движение” нарисованной фигуры.
— Ощущение движения /динамику/ можно усилить резкой сменой направления форм, линий, пятен – от горизонтальных, вертикальных к диагональным и даже спиральным.
Динамика встречается в произведениях изобразительного искусства в пейзаже, анималистическом жанре.
<Рисунок 15>
<Рисунок 16>
— Динамика – это движение.
— Как правило, статика и динамика неразрывно взаимосвязаны, дополняют, или усиливают друг друга, в результате работа в целом выигрывает.
<Рисунок 17>
<Рисунок 19>
— Завершая урок, выполним ряд несложных заданий, в которых по средством статики и динамики выразим различные состояния в мире природы и жизни человека.
Композиции можно взять из двух – пяти фигур, на сюжеты, подсказанные натурой, и условно выраженных силуэтом насекомых, птиц, животных с добавлением трав, цветов.
1. Не срисовывать с вещей, созданных художниками.
2. Полагать на свой неповторимый эмоциональный опыт и фантазию.
Итог: Коллективный анализ работ отмечаются разнообразие и выразительность сюжетов, рассказывают, правильно ли составили композицию.
Отвечают на вопросы:
- Что такое статика и динамика?
- С какими произведениями искусства познакомились?
- В каких произведениях искусства можно встретить статику, а в каких динамику?
Домашнее задание: выполнить композицию, соблюдая симметрию и асимметрию сказку “О царе Салтане”, “Три девицы под окном”. Одно условие не срисовывать.
Асимметрия — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 июля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 июля 2019; проверки требует 1 правка.Асимметри́я[1] (др.-греч. ασυμμετρία «несоразмерность» от μετρέω «измеряю») — отсутствие или нарушение симметрии. Чаще всего термин употребляется в отношении визуальных объектов и в изобразительном искусстве. В художественном творчестве асимметрия может выступать (и очень часто выступает) в качестве одного из основных средств формообразования (или композиции). Одно из близких понятий в искусстве — аритмия. Также термины асимметрия, асимметрический, асимметричный могут означать:
В связи с постоянным делением клеток в организме асимметрия в организмах является обычным явлением по крайней мере в одном измерении наравне с биологической симметрией (также см. Межполушарная асимметрия).
Луи Пастер полагал, что биологические молекулы асимметричны из-за космических [то есть физических] сил, которые осуществляют контроль над их формированием, закладывая свойства (асимметричность), аналогичные своим. Хоть и в его время, и даже сейчас, симметрии в физических процессах придаётся большее значение, так же известны фундаментальные физические асимметрии, начиная с времени.
Полезность для организмов[править | править код]
- Преобладающая рука — асимметрия в развитии навыков людей и животных. Тренировка нервных путей во время обучения навыку с одной рукой (лапой) занимает меньше времени, чем та же тренировка с двумя.[2]

Краб-скрипач, Uca pugnax

Камбала
Природа также предоставляет несколько примеров хиральности в чертах, которые обычно симметричны. Ниже приведены примеры животных с явными признаками асимметрии левой и правой стороны тела:[3]
- У крабов-скрипачей одна клешня большая и одна малая.
- У нарвалов бивень вырастает из левого резца, который может достигать 10 футов и формируется в спираль.
- Камбала эволюционировала плавать всегда одной стороной вверх, в результате чего имеет оба глаза с одной стороны.
- Некоторые виды сов имеют асимметрию в размере и расположении ушей, как полагают, чтобы помочь найти добычу.
- У многих самцов животных (от насекомых до млекопитающих) гениталии асимметричны. Для чего это было нужно эволюции — в большинстве случаев до сих пор загадка.[4]
Тип Porifera состоит из губок, состоящих из нескольких видов, демонстрирующих практически полное отсутствие симметрии тела. Вместо этого они развивались для максимального использования водяного потока через свою центральную полость.
Как индикатор непригодности[править | править код]
Поскольку врожденные дефекты и повреждения, скорее всего, указывают на плохое состояние здоровья организма, дефекты, приводящие к асимметрии часто ставят животное в невыгодное положение, когда речь заходит о поиске партнера. В частности, степень симметрии лица связана с физической привлекательностью, но полная симметрия невозможна и, вероятно, непривлекательна.
В архитектурных стилях, предшествовавших современным, акцент, как правило, делался на симметрии, за исключением когда расположение в экстремальных условиях или исторические разработки вынуждают отойти от классических идеалов. В противоположность этому, некоторые архитекторы современности стали гораздо свободнее использовать асимметрию [6].
Пока большинство мостов используют симметричную форму для внутренней простоты проектирования, анализа, изготовления и экономии в использовании материалов, ряд современных мостов намеренно отошёл от этого, либо в ответ на запросы конкретного участка, либо для создания эффектного дизайна.
Некоторые строения, использующие идею асимметрии
- ↑ асимметрия в Орфографическом словаре и словаре нарицательных имён «Русском словесном ударении» (автор М. В. Зарва, печатное издание М.: ЭНАС, 2001, © Электронная версия, «ГРАМОТА.РУ», 2001—2002)
- ↑ Martin Gardner. The New Ambidextrous Universe: Symmetry and Asymmetry from Mirror Reflections to Superstrings. — 3. — New York: W.H.Freeman & Co Ltd., 1990. — 416 p. — ISBN 0486442446. — ISBN 978-0486442440.
- ↑ Yuh-Nung Jan and Lily Yeh Jan. Asymmetry across species (англ.) // Nature Cell Biology : journal. — 1999. — No. 1. — P. 42—44. — DOI:10.1038/10036. — PMID 10559895.
- ↑ Schilthuizen, Menno. Something gone awry: unsolved mysteries in the evolution of asymmetric animal genitalia (англ.) // Animal Biology : journal. — 2013. — Vol. 63, no. 1. — P. 1—20. — DOI:10.1163/15707563-00002398.
- ↑ В таких случаях может быть использован термин диссимметрия, в противоположность асимметрии — изначального отсутствия симметрии.
- ↑ В. Г. Власов .Тектоника и диссимметрия архитектурной композиции // Электронный научный журнал «Архитектон: известия вузов». — УралГАХУ, 2016. — № 4 (56)

